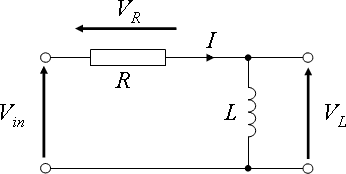
Ao contrário do condensador em que o valor de tensão aumenta com o tempo (durante a carga), aqui é o valor de corrente que aumenta, seguindo o mesmo crescimento logarítmico.
Para o caso a analise da corrente na bobina não é tão importante como a analise de Vr (queda de tensão na resistência). Assim sendo, vou-me debruçar mais sobre este caso, mas que fique claro que a curva de IL é exactamente igual à curva de Vr.
Vamos então ás equações de carga e descarga de uma bobina.
Como já disse as curvas no RL seguem o mesmo crescimento logarítmico que no RC, por isso as equações deste artigo serão bastante semelhantes à do artigo anterior.
Algumas informações extra podem também ser encontradas AQUI.
Tempo de carga de uma bobina:
Equação tempo de carga de uma bobina - medição de VrTempo de descarga de uma bobina:
Equação tempo de descarga de uma bobina - medição de Vr
Vr - queda de tensão na resistência;
Vri - queda de tensão na resistência no valor inicial;
V - tensão de alimentação;
R - valor da resistência;
L - valor da bobina;
t - tempo de carga/descarga;
O que é o Vri?
É o valor de tensão onde se inicia a carga ou descarga. Vamos supor que entramos em fase de carga, então o valor inicial (posto pelo conjunto já calculado do artigo do circuito RC) serão 0s 4.77V e pretende-se então que Vr suba até 7.22V.
Na fase de descarga, Vri é então 7.22V e o Vr até onde deve descer será 4.77V.
Para o circuito de teste em cima, retirei os gráficos seguintes.
Fase de carga:
Gráfico de carga - simulação PROSPICE[/caption]Fase de descarga:
Gráfico de descarga - simulação PROSPICEÉ perfeitamente visível a curva logarítmica dos dois gráficos anteriores.
Agora basta aplicar toda a teoria que já foi discutida no artigo anterior, acerca da oscilação recorrendo a um comparador.
Tendo os dois tempos, o de carga e o de descarga, a equação seguinte é trivial.
Equação para cálculo da frequência
Substituindo por alguns valores já conhecidos, obtemos a equação desejada para chegar ao valor de indutância da bobina.
[caption id="attachment_88" align="aligncenter" width="559"]
Indutância da bobina
Resolvida toda (ou pelo menos a maior parte) a parte teórica, chega o momento de testar tudo junto, usando o LM311 com o mesmo circuito já explicado, tanto em cima, como no artigo anterior.
Circuito de teste com LM311 e RL
Olhando para o circuito em cima e aplicando à equação da frequência, concluímos facilmente que pino 7 teremos de ter uma modulação de pulsos com uma frequência de cerca de 135.22KHz.
Calculo da frequência
Então fazendo a simulação, vamos comparar com este valor teórico e ver se tudo está a funcionar razoavelmente bem.
Simulação em PROSPICEPode ser visto a amarelo na parte inferior da imagem 7.46us, que é o tempo de duração de um período o que resulta numa frequência de 134.048KHz. Bastante próximo, mas esperava que fosse ainda mais próximo.
Ainda assim, vamos aplicar estes 134KHz na equação que realmente interessa, a equação para o cálculo da indutância.
Cálculo do valor da bobina
O que nos diz que com uma resistência de 560R, a produzir uma frequência de 134048Hz, só pode ser uma bobina de aproximadamente 5mH, o que se revela verdadeiro e bastante próximo do valor "ideal".
Por agora, está tudo. Já consigo ter um circuito RL a oscilar e determinar com alguma precisão o valor da bobina, com base no valor da frequência e da resistência em série.
Próximo passo:
Juntar este artigo com o anterior e fazer então um medidor LC.
Já tenho forma de calcular C e agora também já tenho forma de calcular L.
A próxima fase será já desenhar todo o circuito com estas duas partes, respectivos interruptores para separar a leitura de condensadores da leitura de bobinas, etc...
Pode-se dizer que esta era a parte 2 do projecto final e que por agora está concluída!
0 Responses so far.
Enviar um comentário